T14. Pumping-Induced River Drawdown

Pumping from wells besides streams lowers the groundwater level and reduces surface water flow within the stream. This tool helps to estimate the stream depletion rate induced by well pumping.

Start using now!

An understanding of the interaction between groundwater and surface water can help to specify well locations and pumping schedules to minimize these effects (Hunt, 1999). Depending on the considered situation, different analytical equations can be applied to calculate the stream depletion rate. In a system with a stream that fully penetrates the aquifer the analytical equation from Jenkins (1968) can be used with no streambed resistance. The analytical solution of Hantush (1965) includes streambed resistance. In case of a partially penetrating stream with streambed resistance the equation developed by Hunt (1999) can be used. If the system comprises of a partially penetrating stream in an aquitard overlying a pumped aquifer, Hunt (2003) can be applied.

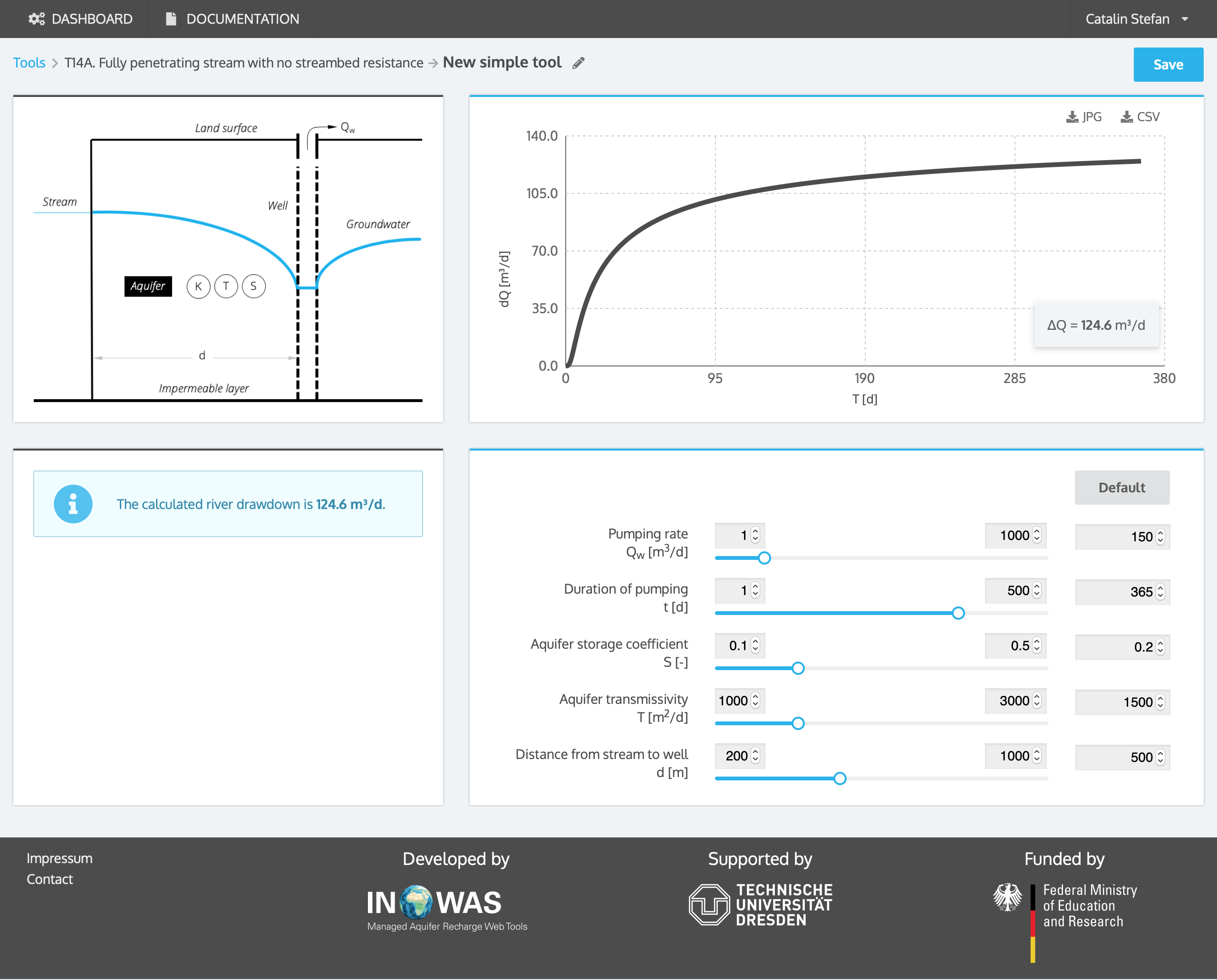
a. Fully penetrating stream with no streambed resistance (Jenkins, 1968)

Figure 1. Sketch of the problem considered by Jenkins (1968) — **Figure 1.** Sketch of the problem considered by Jenkins (1968)

The solution assumes a fully penetrating stream with no streambed resistance between the aquifer and the stream (Reeves, 2008):

$\Delta Q=Q_{w}erfc\left ( \sqrt{\frac{d^{2}S}{4Tt}} \right )$

(eq. 1)

where:

$\Delta Q$	= stream depletion flow rate [L³/T]
$Q_{w}$	= constant well pumping rate [L³/T]
$S$	= aquifer storage coefficient, specific yield or effective porosity [-]
$T$	= aquifer transmissivity [L²/T]
$t$	= time [T]
$d$	= shortest distance between well and stream edge [L]

The main assumptions for the solution include that the horizontal flow dominates vertical flow, the Dupuit assumption is valid, the aquifer is homogeneous, isotrop, has a constant saturated thickness and extends infinitely away from the stream. Furthermore the aquifer is confined or the changes in hydraulic head on the aquifer are small compared to the saturated thickness. The stream is assumed to be straight, infinitely long and fully penetrates the aquifer. The hydraulic conductivity of the streambed is similar or higher than that of the aquifer. There is no streambank storage and the pumping rate is constant (Reeves, 2008).

Example

A pumping well with a distance d of 500 m to a fully-penetrating stream with no colmatation layer is drilled. The well will pump at a rate Q_w of 150 m³/d. The aquifer has a storage coefficient S of 0.2 and a transmissivity T of 1500 m²/d. The stream depletion for the first year of pumping is estimated using the equation developed by Jenkins, 1968. The streamflow will approximately deplete by 124.6 m³/d after one year of operation of the pumping well.

b. Fully penetrating stream with semipervious layer (Hantush, 1965)

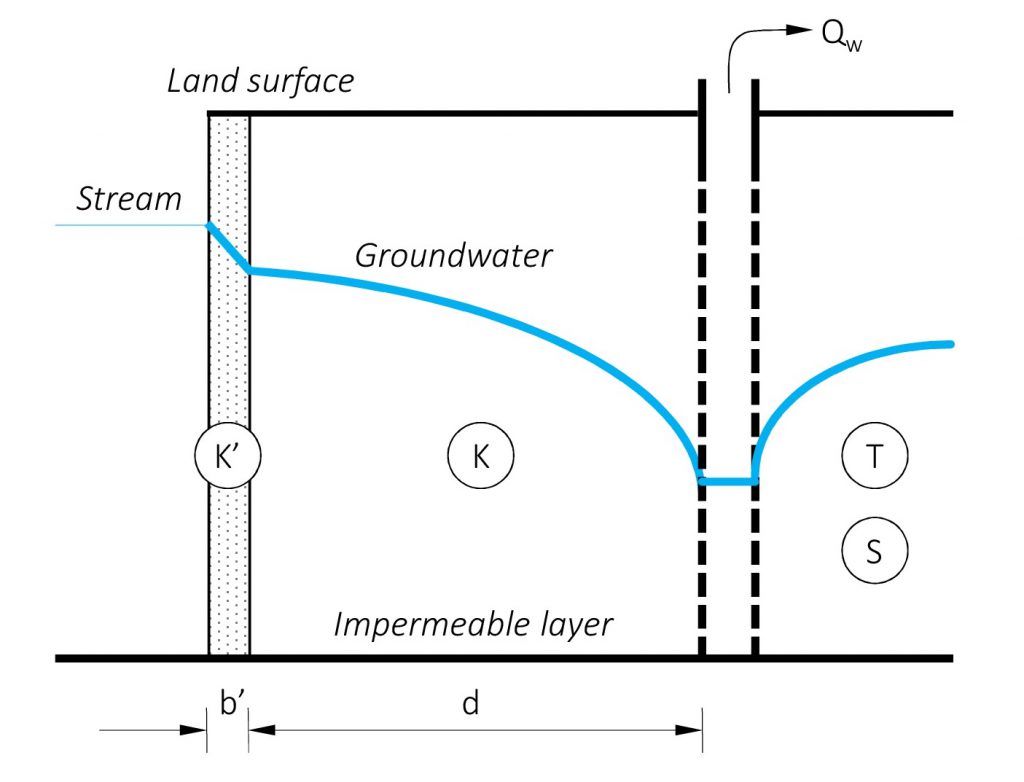
Figure 2. Sketch of the problem considered by Hantush (1965) — **Figure 2.** Sketch of the problem considered by Hantush (1965)

This tool helps to estimate the stream depletion rate induced by well pumping according to Hantush (1965). For a streambed having a fully penetrating vertical layer of semipervious material along the stream edge, Hantush (1965) developed a solution to approximate the occurring stream depletion:

$\frac{\Delta Q}{Q_{w}}= erfc\left ( \sqrt{\frac{Sd^{2}}{4Tt}}) \right )-exp\left ( \frac{Tt}{SL^{2}}+\frac{d}{L}\right )erfc\left ( \sqrt{\frac{Tt}{SL^{2}}}+\sqrt{\frac{Sd^{2}}{4Tt}}\right )$

(eq. 2)

with

$L=\frac{K}{K{}'}b{}'$

$\Delta Q$	= stream depletion flow rate [L³/T]
$Q_{w}$	= constant well pumping rate [L³/T]
$S$	= aquifer storage coefficient, specific yield or effective porosity [-]
$T$	= aquifer transmissivity [L²/T]
$t$	= time [T]
$d$	= shortest distance between well and stream edge [L]
$L$	= streambed leakance [L]
$K$	= aquifer permeability [L/T]
$K{}'$	= permeability of the semipervious layer [L/T]
$b{}'$	= thickness of the semipervious layer [L]

The same assumptions apply as for equation 1 except that the streambed facilitates resistance to flow by having a lower conductivity than the surrounding aquifer.

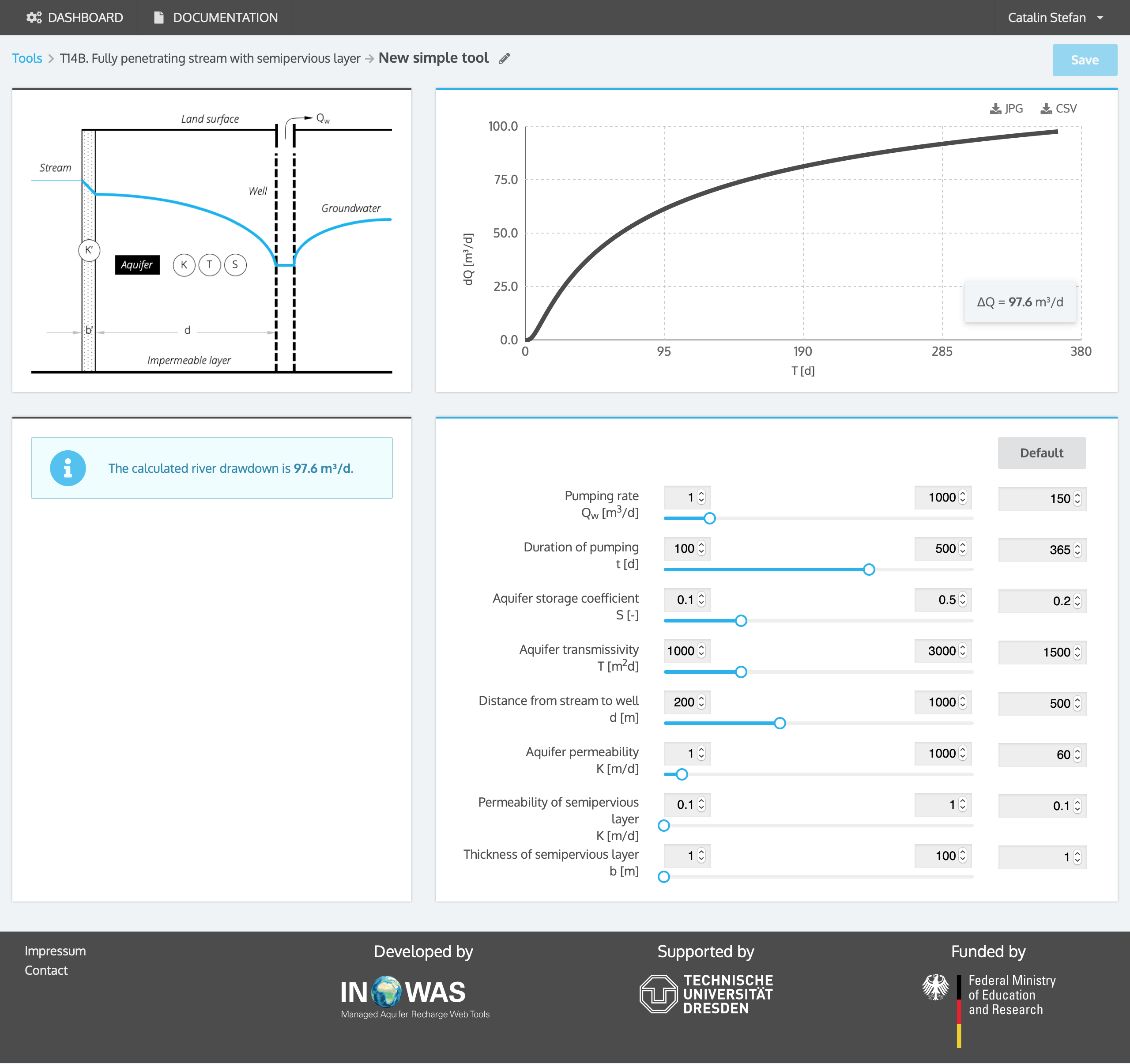
Example

A pumping well with a distance d of 500 m to a fully-penetrating stream with a colmatation layer is drilled. The well will pump at a rate Q_w of 150 m³/d. The aquifer has a storage coefficient S of 0.2, a transmissivity T of 1500 m²/d and a hydraulic conductivity of 60 m/d. The colmatation layer has a thickness b` of 1 m and a hydraulic conductivity of 0.1 m/d. The stream depletion estimated using the equation developed by Hantush, 1965. The streamflow will approximately deplete by 97.6 m³/d after one year of operation of the pumping well.

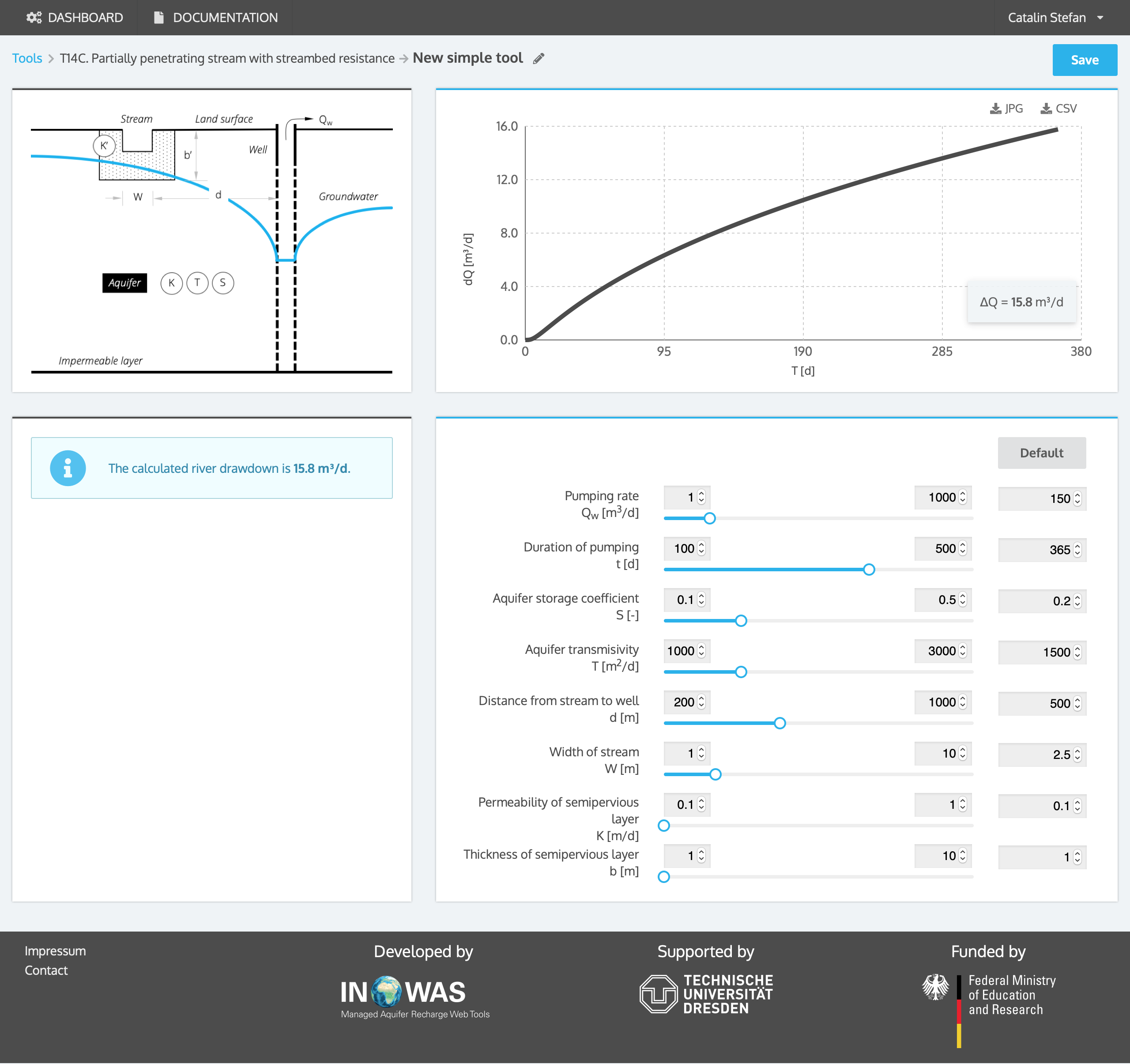
c. Partially penetrating stream with streambed resistance (Hunt, 1999)

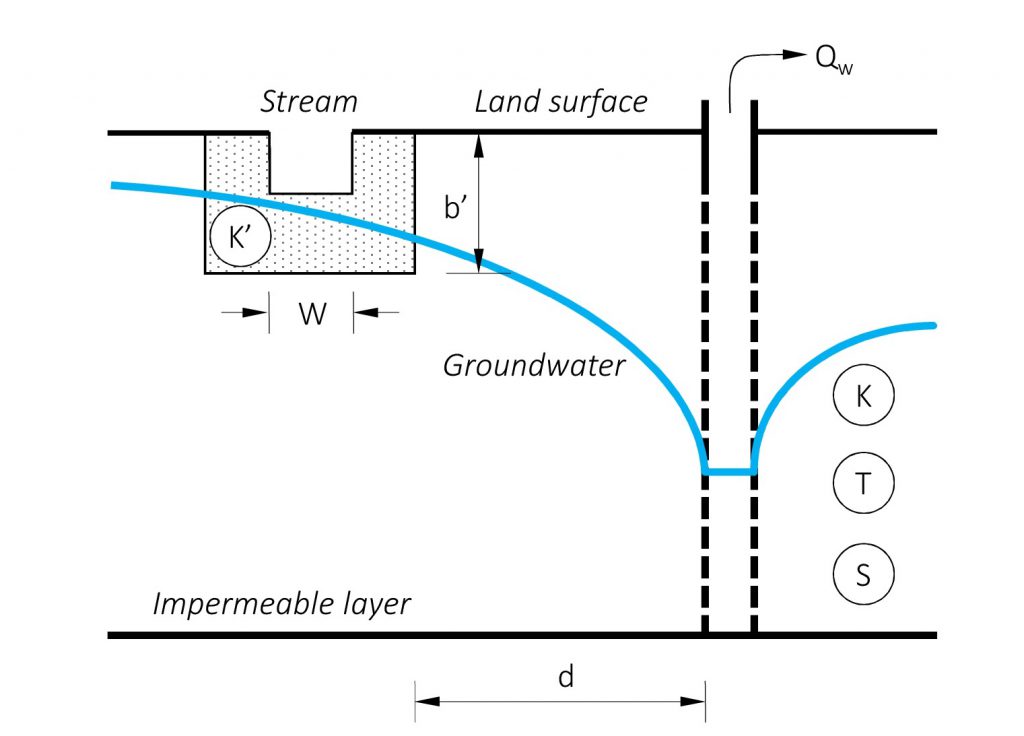
Figure 3. Sketch of the problem considered by Hunt (1999) — **Figure 3.** Sketch of the problem considered by Hunt (1999)

The streamflow depletion in a partially penetrating stream with streambed resistance can be calculated using equation 3 (Hunt, 1999).

$\frac{\Delta Q}{Q_{w}}= erfc \left ( \sqrt{\frac{Sd^{2}}{4Tt}} \right )-exp \left ( \frac{\lambda ^{2}t}{4ST}+\frac{\lambda d}{2T} \right )erfc\left (\sqrt{\frac{\lambda ^{2}t}{4ST}}+\sqrt{\frac{Sd^{2}}{4Tt}} \right )$

(eq. 3)

Equation 3 yields the same as equation 2, if the streambed conductance $\lambda$ is set to: $\lambda =2\frac{T}{L}$ . In general, $\lambda$ is given by: $\lambda =\frac{K{}'W}{b{}'}$ .

$\Delta Q$	= stream depletion flow rate [L³/T]
$Q_{w}$	= constant well pumping rate [L³/T]
$S$	= aquifer storage coefficient, specific yield or effective porosity [-]
$T$	= aquifer transmissivity [L²/T]
$t$	= time [T]
$d$	= shortest distance between well and stream edge [L]
$\lambda$	= streambed conductence term [L/T]
$K{}'$	= permeability of the semipervious layer [L/T]
$b{}'$	= thickness of the semipervious layer [L]
W	= width of stream [L]

The major difference in the assumptions compared to the previous equations is that the stream is assumed to be narrow, extend a small distance into the aquifer and therefore can be modeled as a straight line crossing an infinite aquifer (in horizontal direction). Drawdown may occur in the aquifer on the stream side without the pumping well but the aquifer is assumed to remain in hydraulic contact with the stream which means that pumping does not cause the hydraulic head in the aquifer to be lower than the streambed. Furthermore, streamflow depletion is calculated by Darcy´s Law (Reeves, 2008).

Example

A pumping well with a distance d of 500 m to a partial-penetrating stream with a colmatation layer is drilled. The well will pump at a rate Q_w of 150 m³/d. The aquifer has a storage coefficient S of 0.2 and a transmissivity T of 1500 m²/d. The colmatation layer has a thickness b´ of 1 m and a hydraulic conductivity K´ of 0.1 m/d. The stream has a total width w of 2.5 m. The stream depletion is estimated using the equation developed by Hunt,1999. The streamflow will approximately deplete by 15.8 m³/d after one year of operation of the pumping well.

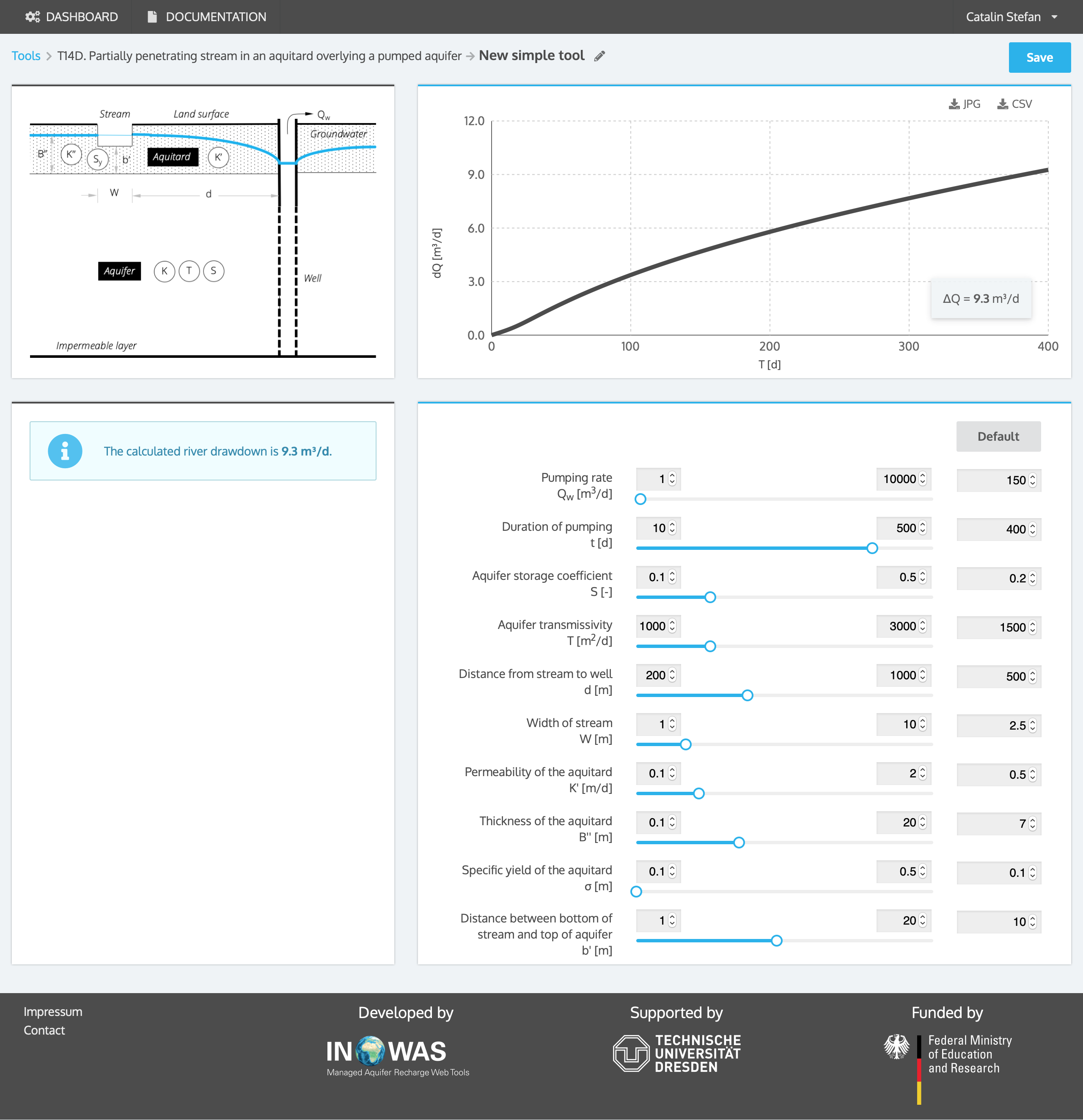
d. Partially penetrating stream in an aquitard overlying a pumped aquifer (Hunt, 2003)

Figure 4. Sketch of the problem considered by Hunt, 2003 — **Figure 4.** Sketch of the problem considered by Hunt, 2003

The following equations can be used to calculate the streamflow depletion in a partially penetrating stream in an aquitard which is overlying a pumped aquifer (Hunt, 2003).

$\frac{\Delta Q}{Q_{w}}= erfc\left (\sqrt{\frac{Sd^{2}}{4Tt}} \right )-exp\left (\frac{\lambda ^{2}t}{4ST}+\frac{\lambda d}{2T}\right )erfc\left (\sqrt{\frac{\lambda ^{2}t}{4ST}}+\sqrt{\frac{Sd^{2}}{4Tt}}\right )-\lambda \int_{0}^{1}F(\alpha ,t)G(\alpha ,t)d\alpha$

(eq. 4)

where

$F(\alpha ,t)=exp\left ( -\frac{d ^{2}S}{4Tt\alpha ^{2}} \right )\sqrt{\frac{Tt}{Sd^{2}\pi }}-\frac{\alpha t\lambda }{2Sd} exp\left (\frac{\lambda d}{2T}+\frac{t\alpha ^{2}\lambda ^{2}}{4ST}\right )erfc\left ( \frac{\alpha \lambda }{2}\sqrt{\frac{t}{ST}}+\frac{d\sqrt{S}}{2\alpha \sqrt{Tt}}\right )$

(eq. 5)

and

$G(\alpha ,t)=\frac{1}{2}\left [ 1-e^{-(a+b)}I_{0}(2\sqrt{ab})+\left ( \frac{b-a}{a+b} \right )\sum_{n=0}^{\infty }\binom{2n}{n}P(2n+1,a+b)\left ( \frac{\sqrt{2ab}}{a+b}^{2n} \right ) \right ]$

(eq. 6)

where

$a=\frac{(K{}'/B{}'')t}{\sigma }(1-\alpha ^{2})$ and

$b=\frac{(K{}'/B{}'')t}{S }\alpha ^{2}$

The streambed leakance $\lambda$ is given by: $\lambda =\frac{K{}'W}{b{}'}$

$\alpha$	= integration variable [-]
$I_{0}()$	= modified Bessel function of zero order [-]
$\binom{2n}{n}$	= binomial coefficient [-]
$P()$	= incomplete Gamma function [-]
$K{}'$	= hydraulic conductivity of the aquitard [L/T]
$B{}''$	= thickness of the aquitard [L]
$\sigma$	= specific yield of the aquitard [-]
W	= stream width [L]
$b{}'$	= distance from bottom of the stream to the top of the leaky aquifer [L]

The assumptions for this solution include that drawdowns both in the aquitard and leaky aquifer are assumed to be small compared to the saturated thickness so that the Dupuit assumption is valid. The aquifer is further assumed to be infinite, homogeneous and has constant thickness. The flow between the leaky aquifer and the aquitard is described by Darcy´s Law and pumping is constant. The stream is infinitely long and stream width is assumed to approach zero so that it can be modeled as a line crossing the infinite aquifer (Reeves, 2008).

Example

A new pumping well with a distance d of 500 m to a partial-penetrating stream is drilled. The aquifer and the stream are seperated by an aquitard with a thickness B´´ of 10 m, a specific yield of 0.1 and a hydraulic conductivity K´of 0.5 m/d. The well will pump at a rate Q_w of 150 m³/d. The aquifer has a storage coefficient S of 0.2 and a transmissivity T of 1500 m²/d. The stream has a total width w of 2.5 m. The distance between the bottom of the stream and the top of the leaky aquifer b´is 7 m. The stream depletion is estimated using the equation developed by Hunt,2003. The streamflow will approximately deplete by 9 m³/d after one year of operation of the pumping well.

REFERENCES

- Hantush, M.S., 1965. Wells near streams with semipervious beds. Journal of Geophysical Research 70, 2829–2838. doi:10.1029/JZ070i012p02829
- Hunt, B., 1999. Unsteady stream depletion from ground water pumping. Groundwater 37, 98–102. doi:10.1111/j.1745-6584.1999.tb00962.x
- Hunt, B., 2003. Unsteady Stream Depletion when Pumping from Semiconfined Aquifer. Journal of Hydrologic Engineering 8(1), 12–19. doi:10.1061/(ASCE)1084-0699(2003)8:1(12)
- Hunt, B., 2014. Review of Stream Depletion Solutions, Behavior, and Calculations. Journal of Hydrologic Engineering 19(1), 167–178. doi:10.1061/(ASCE)HE.1943-5584.0000768
- Jenkins, C.T., 1968, Computation of rate and volume of stream depletion by wells: U.S. Geological Survey Techniques of Water-Resources Investigations, book 4, chap. D1, 17 p.
- Reeves, H.W., 2008. STRMDEPL08—An extended version of STRMDEPL with additional analytical solutions to calculate streamflow depletion by nearby pumping wells (No. 2008–1166), USGS Open-File Report.
- STRMDEPL08 (standalone): http://mi.water.usgs.gov/software/groundwater/strmdepl08/
- STRMDEPL08 (web-based): http://mi.water.usgs.gov/software/groundwater/CalculateWell/index.html